
Using loop invariants for verification in Reach
Let’s face it, writing smart contracts is really hard. Writing a fully decentralized, distributed, trustless system is super difficult but how can we be sure that the contract does what it is supposed to do? How do we know that the contract doesn’t lock away 1000 ALGO for its owners after a certain point of time. How do we know that the smart contract doesn’t spend more money than it has? We would definitely like to avoid a situation like the infamous DAO hack.
Enter Reach, a domain specific language (DSL) which makes it easy to write and verify smart contracts. Yes, Reach programs can be formally verified to prove facts that our smart contract does not lock away our funds or does not spend more than it has. You can even verify richer properties such as all participants should have the same contribution in a pool. Excited to learn more? So dive right in.
The importance of verification for smart contract writers and businesses cannot be stressed enough. In the world where tools like Reach are available, having a formally verified contract with strong guarantees should be the baseline. This way every participant in the system can trust the code and thus we can safely usher in a new generation of dApps.
But, even with the ability to automatically verify programs, loops are one of the trickier parts of a program to verify. This is because a loop can execute an infinite number of times depending on the condition. Thus, we cannot have an algorithm that can tell us if every loop will execute correctly. When a program has a finite number of steps, we can just list all possible behaviors and verify them but in the case of loops, there are infinite such possibilities. But as we all know, loops are the corner-stone of all programs we right. Most smart contracts are meant to be executed indefinitely - so hey, there’s a loop right there. We might have any number of participants, so we’d like to loop over them and so on. You get the point - writing a real-world smart contract without loops is not possible. Thus, we need a way to verify loops and that method is called using a loop invariant. If you are interested in the definitions and intuition about loop invariants, you can read GeeksForGeeks, Wikipedia or StackOverflow. Don’t worry, we will develop the intuition and define what a loop variant throughout this tutorial, so you don’t have to be worry if you don’t have a background yet!
The agenda for this tutorial is as follows -
- Discuss the difference between testing and verification
- See what loop invariants are and how they are used to verify loops
- Write a skeleton program to test our Reach setup
- Write a simple (incorrect) loop and its invariant and see how it fails verification
- Correct the previous loop and see the verification succeed
- See how loop invariants help us prove assertions that hold after the loop completes
- Discuss how to choose the right loop invariant required for verification
- Write a nested loop and its invariant
- Study a (simplified) real-world application of loops and invariants
- Thanks!
Requirements
All you need to follow this tutorial is a working Reach compiler. The setup instructions are here - https://docs.reach.sh/tut-1.html
Background
Since this is an intermediate tutorial, you should be comfortable with the following Reach topics -
1. Reach language and execution model
2. Reach syntax
3. Reach steps - Steps, Local Steps and Consensus Steps
4. Reach assertions
Broadly speaking, you should be familiar with the ideas of immutable variable bindings, continuations of statements and loop syntax. You should also have a grasp of the local steps and consensus steps which form parts of the Reach program. Along with this, knowing how assert statements in Reach are used for static verification would also be helpful.
While we do not assume any background in formal verification, it would be good to have some idea of why formal verification is necessary. In recent years, we have seen multiple attacks where some flaw in smart contract logic has been exploited for malicious actions such as freezing or stealing funds, which could possibly have been avoided by formal verification. Some notable examples are -
Steps
Let’s get started with this tutorial on using loop invariants to verify loops in Reach. We will start from the basics and hopefully by the end, you would have developed a good intuition on how loop invariants actually work, so you can go out there and verify your own programs!
An important point to note before we start the tutorial is that all the examples are heavily simplified to highlight the loops and their verification. Real-world applications will have significant additional content, but the central idea of verifying loops should stay the same.
We will only start writing Reach code from Step 3 onwards. The code snippets in Sections 1 and 2 are only for examples. Inline code blocks will be displayed as var x = 10 and code blocks will be written as -
var x = 10 // L1
The necessary lines will have labels so that we can refer to them in text. Here when we say L1, we are referring to the line var x = 10. All steps have an associated folder in the Github repository from step-3 to step-8.
So let’s get started! Hopefully you have fun reading this tutorial and learn something along the way!
1. Testing vs Verification
It would be good to first learn a little about how testing differs from verification and why it is important that we verify our programs. Testing and verification are different approaches to checking the correctness of programs which enables us to be confident that the program actually does what it is supposed to do.
Let’s start by discussing a very simple example. Let’s say we write this simple function that multiplies a number by 2 and returns the value -
const multiplyByTwo = (num) => {
if(num == 0) {
return 1;
} else {
return num * 2;
}
}
As we can see, the code is incorrect. Now, the typical way to write unit tests for this would be -
assert(multiplyByTwo(2) = 4);
assert(multiplyByTwo(4) = 8);
Note that this test suite would not capture the error. Thus testing is limited as it will only check correctness for the inputs we provide. Whether we are able to design a completely exhaustive test-suite or not is up to the programmer, but for most cases a fully exhaustive enumeration of all cases is not possible!
This is where verification comes in. By using logical relations and theorems that we know about math (such as for all numbers n, n * 0 = 0), we can automatically test our function for all inputs. Please note that we are not manually testing all values. Logical reasoning allows us to verify that the code is wrong for an input, and our verifier will provide the counterexample. In this case, the correctness condition would be -
forall n , multiplyByTwo(n) == n * 2
The Reach compiler converts every program into logical formulae and then verifies if the programmer provided assertions hold or provides a counterexample when it is wrong.
2. Loop invariants
Now loops are funny because verifying arbitrary loops is actually impossible. Loops have 2 different components we need to verify. Does a loop terminate and if it does, does it terminate correctly? Turns out it is impossible to answer this question in the general case. So let us just stick to verifying loops that we know terminate. So if a loop terminates (we hope it does!), does it terminate correctly?
Let’s look at this simple program -
var x = 0;
while(x < 5) {
x = x + 1;
}
assert(x == 5);
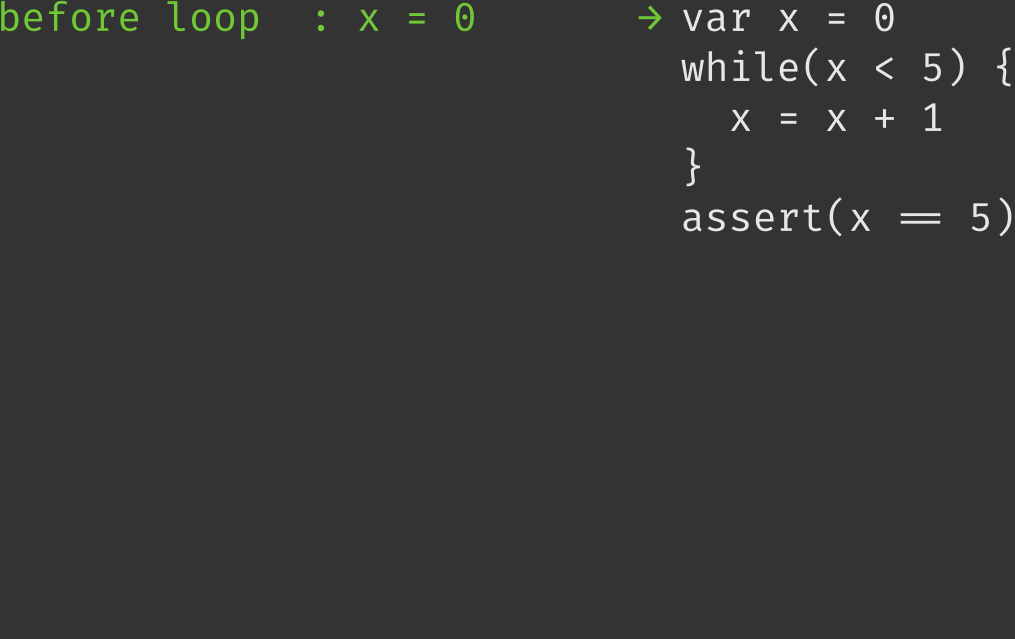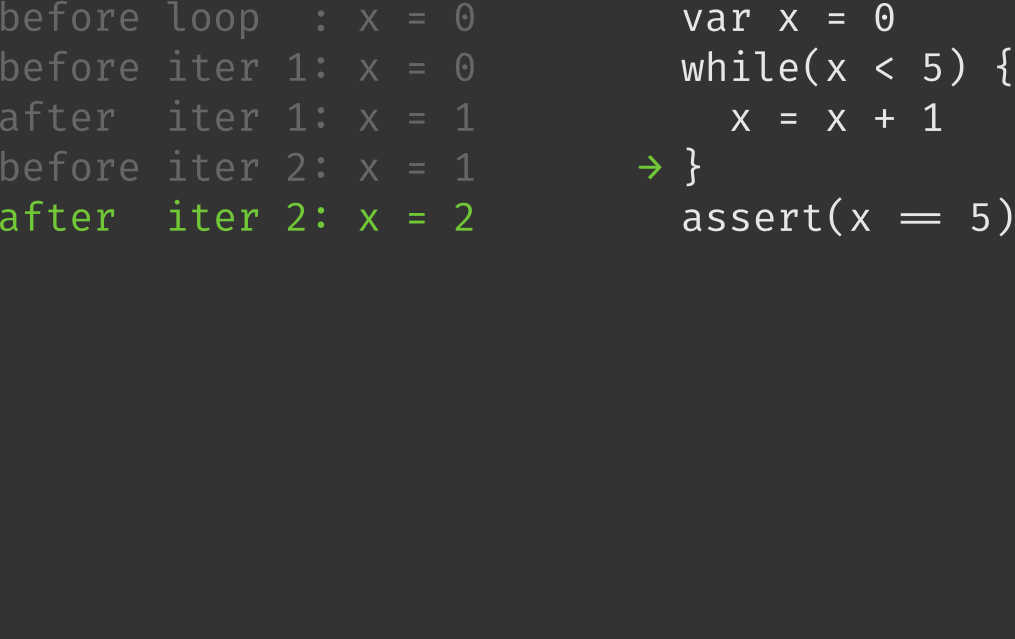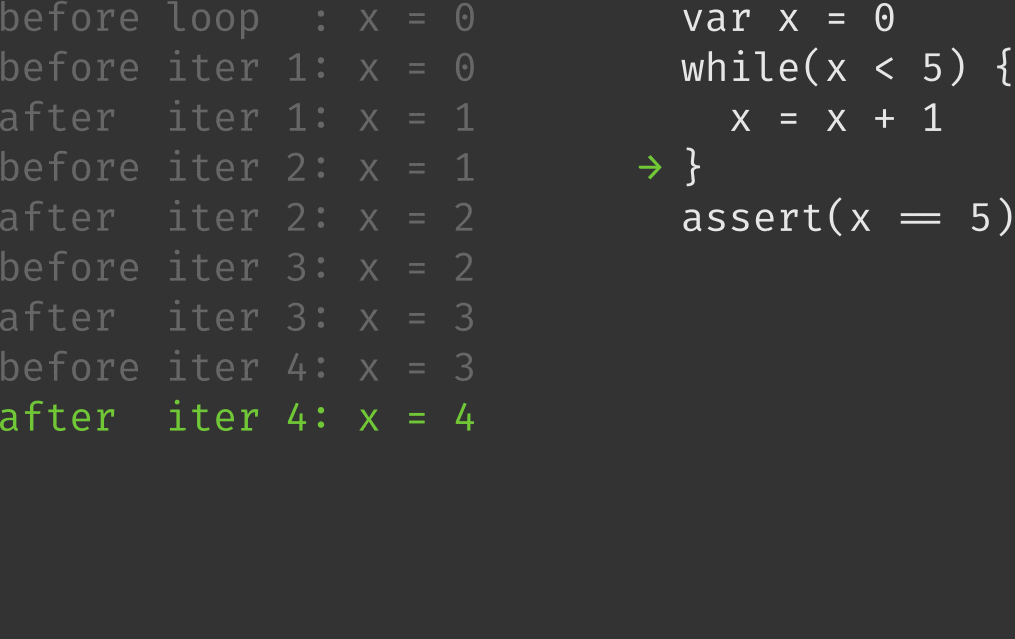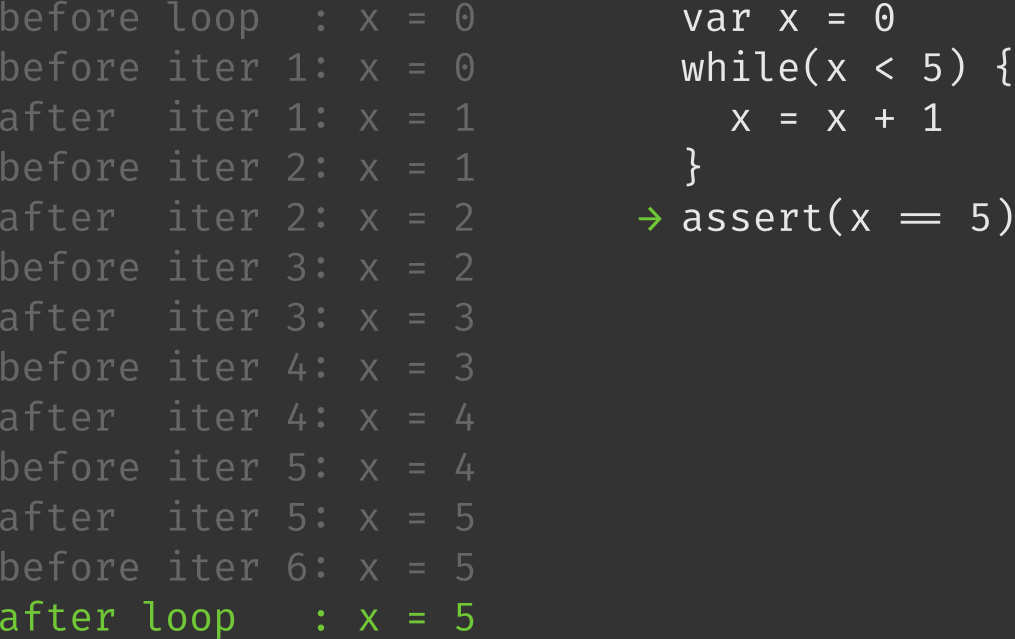
By intuition, we are clear that the loop terminates correctly. Before the loop, x = 0 and after the loop x = 5. How do we formally show that the loop actually takes us from x = 0 to x = 5. Let’s look at the iterations to understand better -
iter 1: x = 0 , x < 5 is true, loop iteration is executed
iter 2: x = 1 , x < 5 is true, loop iteration is executed
iter 3: x = 2 , x < 5 is true, loop iteration is executed
iter 4: x = 3 , x < 5 is true, loop iteration is executed
iter 5: x = 4 , x < 5 is true, loop iteration is executed
iter 6: x = 5 , x < 5 is false, loop exits
Intuitively, if we could formally verify that a general step of the iteration is correct, then the entire loop should be correct. Thus, we need a condition which holds for each iteration. This property is called the loop invariant. If we know some condition L, holds for every iteration of the loop, we can be confident it holds at the end of the loop. Thus given a loop invariant L and a loop condition C, we can show that the required state after the loop is !C && L. The intuition behind this is that at the end of the loop C does not hold, thus the loop exits and the loop invariant L continues to hold. In our case the loop invariant L is x <= 5 and C is x < 5. Let’s look at the iterations -
iter 1: x = 0 , x < 5 is true, x <= 5 is true
iter 2: x = 1 , x < 5 is true, x <= 5 is true
iter 3: x = 2 , x < 5 is true, x <= 5 is true
iter 4: x = 3 , x < 5 is true, x <= 5 is true
iter 5: x = 4 , x < 5 is true, x <= 5 is true
iter 6: x = 5 , x < 5 is false, x <= 5 is true

As we can see, the program terminates with !C = !(x < 5) = x > 5 and L = x <= 5, which means x = 5, satisfying our assertion assert(x == 5). Thus, the loop invariant gave us a way of verifying what the state of the program after the execution of the loop will be.
3. Setup and Scaffolding
Refer to the folder step-3 for the full code.
In this step, we will setup a basic program which will run as a sanity test to check that everything is in order. Start by creating an index.mjs file with the following content -
import { loadStdlib } from '@reach-sh/stdlib';
import * as backend from './build/index.main.mjs';
const stdlib = loadStdlib(process.env);
(async () => {
console.log("[LOG] App: starting application");
const startBalance = stdlib.parseCurrency(1000);
const accA = await stdlib.newTestAccount(startBalance);
const accB = await stdlib.newTestAccount(startBalance);
const ctcA = accA.deploy(backend);
const ctcB = accA.attach(backend, ctcA.getInfo());
const ParticipantInterface = (who) => ({
log: (msg) => console.log(`[LOG] ${who}: ${msg[0]} ${msg[1]}`)
});
await Promise.all([
backend.A(ctcA, {
...ParticipantInterface("A")
}),
backend.B(ctcB, {
...ParticipantInterface("B")
}),
]);
console.log("[LOG] App: exiting application");
})();
This is just a standard frontend application with some functions to log messages from the backend. Then create a file named index.rsh with the following content -
'reach 0.1';
const ParticipantInterface = {
log: Fun(true, Null)
};
export const main = Reach.App(() => {
const A = Participant('A', {
...ParticipantInterface
});
const B = Participant('B', {
...ParticipantInterface
});
deploy();
A.interact.log(["Testing app", 0]);
B.interact.log(["Testing app", 0]);
exit();
});
Running reach run in the folder with these 2 files should then build the entire application and give you the following output at the end -
...
[LOG] App: starting application
[LOG] A: Testing app 0
[LOG] B: Testing app 0
[LOG] App: exiting application
...
So if you could follow till here and everything is in order, we are ready to dive into the tutorial!
4. A simple (incorrect) loop and its invariant
Refer to the folder step-4 for the full code.
We will start by writing a simple loop in Reach and its invariant. The informal specification of the program is that a participant A transfers tokens in increments of 10, until the balance hits 100. Since the loop implementation is incorrect, the Reach verifier will fail. Modify index.rsh and add the following content -
...
deploy();
// Enter consensus step to execute while loop
A.publish();
var [] = []; // L1: not binding any mutable loop variables
invariant(balance() <= 100); // L2: loop invariant L = balance() <= 100
while(balance() < 100) { // L3: loop condition C = balance() < 100
commit(); // L4: commit consensus step, so all participants agree on control flow
A.pay(10); // L5: transfer tokens and enter consensus step
A.interact.log(["A paid", 10]); // L6: log the transfer
[] = []; // L7: no updates to mutable variables
continue; // L8: continue the loop
}
// Transfer tokens back to A
transfer(100).to(A);
commit();
// Exit program
exit();
});
Let’s break down our loop syntax. The line numbers
- Since bindings are immutable in Reach, we need to declare variables that we are going to mutate inside the loop. This is done in
L1. Here we do not declare any such variable. - We declare our loop invariant in
L2. - We declare the while loop condition in
L3. L4-L6are the body of the loop. In this body, we just transfer 10 tokens.- Before continuing the loop, we need to declare the mutable updates for the loop variables. This is done in
L7. We do not update any variables here. L7continues onto the next loop iteration.
Note that the continue needs to be preceded (dominated by) by a consensus transfer statement. In this program, the pay at L5 serves that role. Take a moment to study the loop and figure out where we can go wrong. The Reach verifier will tell us pretty soon, but it is fun to simulate the various situations in your head and figure out what can break!
Once you are done thinking run the command reach run. If you have followed until here, you should see this output -
Verification failed:
when ALL participants are honest
of theorem: while invariant after loop
at ./index.rsh:18:3:invariant
// Violation Witness
const balance(0)/58 = <loop variable>;
// ^ could = 91
// from: ./index.rsh:19:3:while
// Theorem Formalization
const v92 = (balance(0)/58 + 10) <= 100;
// ^ would be false
while invariant after loop(v92);
The Reach verifier reports that we would have a violation of the while invariant after loop and gives us the situation where it could break. If the balance is 91 before an iteration, then the iteration would break our invariant. Woah, this Reach thing is pretty cool, huh! While you could argue that since we started the program with balance 0, this situation can never arise. But remember, Reach verifies the loops for arbitrary iterations. Thus it could not verify that for all inputs, the loop iteration would not break our invariant and thus reported the counterexample.
I hope this helps you appreciate how useful formal verification can be. In the next section, we will correct our loop and stop the Reach verifier from complaining.
5. The loop corrected
Refer to the folder step-5 for the full code.
Its time now to carefully reconsider our code and then correct it. So here’s the corrected loop -
...
var [] = []; // L1: not binding any mutable loop variables
invariant(balance() <= 100); // L2: loop invariant L = balance() <= 100
while(balance() < 100) { // L3: loop condition C = balance() < 100
if(balance() > 90) { // L4: pay difference if value > 90
commit();
const toPay = 100 - balance();
A.pay(toPay);
A.interact.log(["A paid", toPay]);
} else { // L5: else pay 10 tokens
commit();
A.pay(10);
A.interact.log(["A paid", 10]);
}
[] = []; // L6: no updates to mutable variables
continue; // L7: continue loop
}
...
As before, let’s see a quick breakdown -
1. The lines L1, L2, L3 are the same as before
2. L4 enters a new conditional branch. We check if the balance() is less than 10 tokens away from 100. If yes, A pays the difference else A pays 10.
3. L6 and L7 are the same.
Now if we run the compiler, we should get the following output -
Verifying knowledge assertions
Verifying for generic connector
Verifying when ALL participants are honest
Verifying when NO participants are honest
Verifying when ONLY "A" is honest
Verifying when ONLY "B" is honest
Checked 29 theorems; No failures!
Yay! The Reach verifier verified our loop. As an additional exercise, try increasing the balance() to some non-zero number by sending a few tokens before the loop, to see your if-else conditional statement in action.
6. Verifying post-loop assertions
Refer to the folder step-6 for the full code.
All right, now we can verify that our loop iterations don’t break the loop invariant. Now think back to Step 2. We discussed that at the end of a loop we should have !C && L to be true. Thus in our running example, this would allow us to verify that the balance at the end is 100 since !C = !(balance() < 100) = balance() > 100 and L = balance() <= 100, which implies balance() == 100. Let’s modify our program to add this assertion -
...
var [] = []; // not binding any mutable loop variables
invariant(balance() <= 100); // loop invariant L = balance() <= 100
while(balance() < 100) { // loop condition C = balance() < 100
if(balance() > 90) { // pay difference if value > 90
commit();
const toPay = 100 - balance();
A.pay(toPay);
A.interact.log(["A paid", toPay]);
} else { // else pay 10 tokens
commit();
A.pay(10);
A.interact.log(["A paid", 10]);
}
[] = []; // no updates to mutable variables
continue; // continue loop
}
assert(balance() == 100);
...
As we can see, the only new addition is the assert(balance() == 100). Since our loop invariant and loop termination implies this assertion, the verifier can verify this statement.
7. Choosing the right invariant
Refer to the folder step-7 for the full code.
But a good question to ask would be - “Is this the only loop invariant that can be used here?”. The answer to that is no. There could be a countless number of loop invariants that hold for the loop iterations. But, it is important to choose the right invariant that allows us to verify the post-loop assertions. For example, the following program -
var [] = []; // not binding any mutable loop variables
invariant(balance() <= 200); // loop invariant L = balance() <= 200
while(balance() < 100) { // loop condition C = balance() < 100
if(balance() > 90) { // pay difference if balance > 90
commit();
const toPay = 100 - balance();
A.pay(toPay);
A.interact.log(toPay);
} else { // else pay 10 tokens
commit();
A.pay(10);
A.interact.log(10);
}
[] = []; // no updates to mutable variables
continue; // continue loop
}
assert(balance() == 100);
The only difference here is that our loop invariant is balance() <= 200. In this case, when we run the compiler we see the following output -
Verification failed:
when ALL participants are honest
of theorem: assert
at ./index.rsh:41:9:application
// Violation Witness
const balance(0)/78 = <loop variable>;
// ^ could = 101
// from: ./index.rsh:19:3:while
// Theorem Formalization
const v102 = balance(0)/78 == 100;
// ^ would be false
assert(v102);
So even though the loop verification is successful (as the loop invariant holds over each iteration), the assertion could not be verified. Try commenting out the assert to see that the verified successfully completes verification. Thus, it is important to choose the right loop invariant which allows us to verify our post-loop assertions.
8. Nested loops and mutable loop variables
Refer to the folder step-8 for the full code.
In this section, we are going to write a nested loop which actually uses and mutates loop variables. We will see how we our invariant for the inner loop needs to refer to the variables of the outer loop.
The informal specification for our problem is that our loop executes for a fixed number of rounds. In each round, A pays a round dependent value and B matches that value by paying in increments of 50. We want to verify the assertion at the end that the amount contributed by A is the same as the amount contributed by B. Let’s look at the loop -
...
var [shareA, shareB, round] = [0, 0, 0]; // L1: binding loop variables
invariant(shareA == shareB); // L2: loop invariant
while(round < 5) { // L3: loop condition
A.interact.log(["Round: ", round]);
A.interact.log(["Share A", "Share B"]);
A.interact.log([shareA, shareB]);
commit();
const roundValue = round * 100; // L4: amount A pays
A.pay(roundValue);
A.interact.log(["A pays: ", roundValue]);
var [shareBL] = [shareB]; // L5: binding loop variables for nested loop
invariant(shareBL <= shareA + roundValue); // L6: loop invariant
while(shareBL < shareA + roundValue) { // L7: loop condition
const toPayB = shareA + roundValue - shareBL; // L8: difference B needs to pay
if(toPayB < 50) { // L9: B pays difference if less than 50
commit();
B.pay(toPayB);
B.interact.log(["B pays: ", toPayB]);
[shareBL] = [shareBL + toPayB];
continue;
} else { // L10: else B pays 50
commit();
B.pay(50);
B.interact.log(["B pays: ", 50]);
[shareBL] = [shareBL + 50];
continue;
};
}/
assert(shareBL == shareA + roundValue); // L11: inner loop assertion
[round, shareA, shareB] =
[round + 1, shareA + roundValue, shareBL];
continue;
}
assert(shareA == shareB); // L12: outer loop assertion
...
I have only labeled the important statements. Let’s break it down -
1. In L1, we bind three variables round, shareA, shareB representing the rounds completed, A’s contribution and B’s contribution.
2. L2 and L3 are the loop invariant and loop condition respectively. Note that since our post-loop assertion is shareA == shareB on L12, this invariant is sufficient.
3. In L4, we compute the round-dependent value A pays.
4. At L5, we start the nested loop by binding a loop variable for the inner loop which is initialized to B’s contribution upto this point.
5. L6 is the loop invariant for the inner loop. Note that, the loop invariant refers to variables that are defined outside the loop. Intuitively, we want to say that after every iteration we are less or equal to A’s contribution upto this point.
6. L7-L10 are the inner loop condition and the loop body
7. L11 is the inner loop assertion stating that B’s contribution after the loop is equal to A’s contribution up to this point.
8. L12 is the outer loop assertion stating that after every iteration, A and B have contributed the same amount.
Here, we are saying that if in every outer loop iteration, if B matches what A contributes, then their share stays equal. After every inner loop iteration, B increments its contribution to match A and exits when the contribution matches. Thus, we have performed verification across nested loops.
Additional challenge: Try to change the programs to prove the assertion shareA == shareB && shareA + shareB == balance(). The solution is in folder step-8.1.
9. A real-world example
Refer to the folder step-9 for the full code.
Having seen how we can use loop invariants for verification, let’s look at a very simple example which can illustrate how this can be used. Some of the most popular smart contracts are automated market makers (AMM’s) such as Uniswap, which are to used to build decentralized exchanges. At the core of these contracts, lies something called a Constant Function Market Maker (CFMM) which decides the price and quantity of tokens that are exchanged. A CFMM is just a relation between token quantities that needs to be maintained at a constant value.
While there are a wide range of CFMM’s, the most basic one is the constant sum formula. This says that for two tokens x and y, the sum of their values in reserve should stay the same. Thus, if a participant wants to withdraw some number of tokens x, they need to provide equal number of tokens y, to maintain the sum as constant. This can be written as x + y = k. Thus, this beautifully lends to be a loop invariant, if we treat each trade as an iteration of a while loop. Let’s look at a very simple implementation -
...
const k = 100 + 10;
var [poolA, poolB, round] = [100,10,0];
invariant(balance() == 0 && poolA + poolB == k);
while(round < 5) {
commit();
A.interact.log(["Round: ", round]);
const toSwapA = 10;
const balanceA = poolA - toSwapA;
const balanceB = k - balanceA;
const toSwapB = balanceB - poolB;
A.publish();
A.interact.log(["Swap A", "Swap B"]);
A.interact.log([toSwapA, toSwapB]);
A.interact.log(["Balance A", "Balance B"]);
A.interact.log([balanceA, balanceB]);
[round, poolA, poolB] = [round + 1, balanceA, balanceB];
continue;
}
assert(poolA + poolB == k);
...
The code is pretty much self-explanatory. But with the power of Reach, we can see how easily we can codify an important fundamental principle of our algorithm and verify it formally.
10. Thanks!
That’s all folks! If you really did stick to the end and even if you didn’t, I really appreciate you taking the time to read it. Hopefully it taught you something useful and you will use some of these ideas in your own projects. You can check out the full code at - https://github.com/anmolsahoo25/reach-loop-verification